Fill the grid subject to product, sum and knight move constraints

Question

Using the numbers 2, 3, 4, ... 19 each exactly once, fill some of the empty squares in the grid with a number so that the product of the numbers in each row is as shown, as is the sum of the numbers in each column.

Also a chess knight starting on the square numbered 1 must be able to make a valid move and land on the square numbered 2 and from there it must be able to make a valid move and land on the square numbered 3 then jump to 4 then 5 ... finally landing on the square numbered 20.

---

Attribution: June 2024 issue of MathsJam Shout. (Puzzle by Paul Taylor)

Answer 1

The obvious first step is to list the prime factorization of each product. Red cells mark the prime factors that are already used. Also, let's subtract the placed numbers from the sums for easier tracking.

The prime factors 11, 13, 17, and 19 appear exactly once in the range from 1 to 20. Therefore, we know that 17 appears in R2, 19 in R3, and 11 and 13 in R4. We can immediately place 19, which must be a knight away from the given 20.

Let's draw a checkerboard. Since a knight's move connects a white cell and a green cell, all odd numbers appear on green cells and all even numbers appear on white. Now we can place 17: it can only go to either R2C1 or R2C3, but it cannot go to C1 since the remaining sum is not large enough, so it goes to R2C3. 18 goes to the only remaining cell that is a knight away from both 17 and 19, which is R4C4.

15 can only appear on R3 because R5 does not have the prime factor 3. Since there is only one green cell left on R3, 15 goes there. There are two cells that are a knight away from both 17 and 15: R1C5 and R4C2. Since R4 does not contain enough 2s, 16 goes to R1C5.

At this point, we can identify which numbers go to which row. There are two multiples of 5 remaining (5 and 10), both of which go to R5 (by the prime factors 5), and since 2 cannot be on R5 (too far away from 1), the remaining number must be 14. R1 must have 2 and 7, which places 2 immediately (only one white cell left) and 3 (only one cell left that is a knight away from 2).

On R3, only white (even) cells are available, so the remaining number must be a single 6. 8 must be a knight away from 7, which places it on R2 (because R3 is not available). The other cell on R2 becomes 12.

The remaining numbers are 4 and 9, which fit the remaining product 2^2 3^2 on R4. 4 goes to the only white cell left.

Placing 7 on C2 makes the C2 sum impossible (because 1 is already used), so it goes to C4. 8 goes to C2 by a knight move from 7, and 12 goes to C4. By C4 sum, 5 goes to C4 as well.

There is only one way to make the sum of 9 using the remaining numbers: 9 itself. So 9 goes to C1. 10 and 11 are placed by knight's moves; 13 and 14 go to the only remaining cell with nonzero sums respectively; 6 goes to C5 to make the final sum correct.

Answer 2

First find a place for 19:

19 is a factor of 1710 = 19 x 90, this puts 19 in row 3. It must be a knight's move from 20, in column 2. Number 19 is placed in row 3, column 2.

Then for 17:

17 is a factor of 4896 = 17 x 288, this puts 17 in row 2. It cannot be in column 1, as this would exceed the given sum. Column 3 is the only other odd cell available in row 2. Number 17 is placed in row 2, column 3.

Then for 18:

18 must be a knight's move from both 17 and 19. Number 18 is placed in row 4, column 4.

For 11, 12, 13:

11 and 13 are factors of 92664 = 11 x 13 x 648. They are both in row 4. Neither can be in column 1, so they must be in columns 3 and 5. The number 12 must be a knight's move from each: Number 12 is placed in row 2, column 4.

For 14, 15, 16:

With 13 in row 4, 14 must be in row 5, column 3 or 5. From either of those cells, number 15 is placed in row 3, column 4. With 15 and 17 in place, 16 must be a knight's move from both. The column sum would be exceeded in column 2, so number 16 is placed in row 1, column 5.

Continuing:

Row 2 contains 17, 12 and 1. The product of the remaining numbers in this row is 24. This requires two numbers, one of which must be odd. This can only be 3 x 8.
Number 3 is placed in row 2, column 1.
Number 8 is placed in row 2, column 2. Number 7 is placed in row 1, column 4.

Row 3 contains 19 and 15. The product of the remaining numbers in this row is 6. Number 3 is already placed in row 2, so the only other number in row 3 is 6.
Number 2 is placed in row 1, column 3. (A knight's move from both 3 and 1)
Number 4 is placed in row 4, column 2.
Number 5 is placed in row 5, column 4.

Number 9 is placed in row 4, column 1.
Number 10 is placed in row 5, column 3.
Number 11 is placed in row 4, column 5.
Number 13 is placed in row 4, column 3.
Number 14 is placed in row 5, column 5.
Number 6 is placed in row 3, column 5.

The completed grid:

 20 ..  2  7 16
  3  8 17 12  1
 .. 19 .. 15  6
  9  4 13 18 11
 .. .. 10  5 14
 

Answer 3

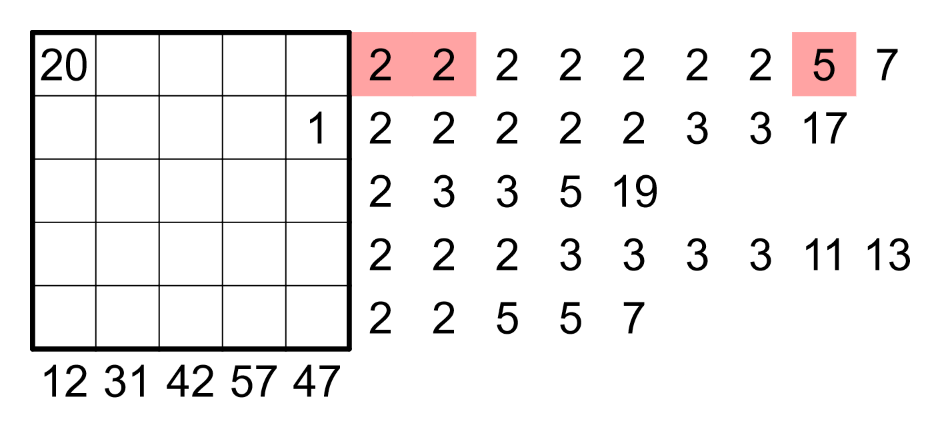
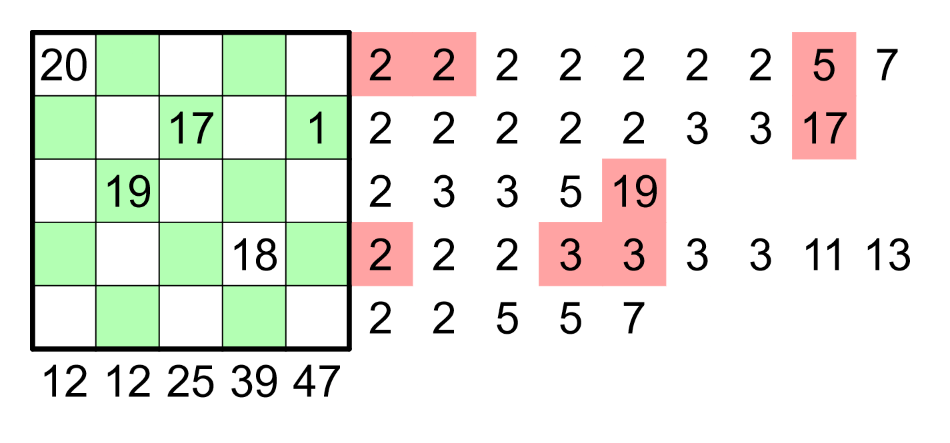
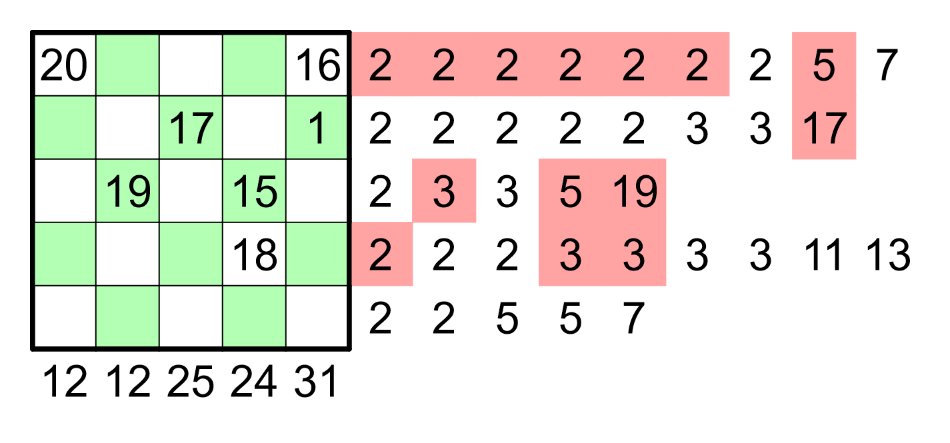
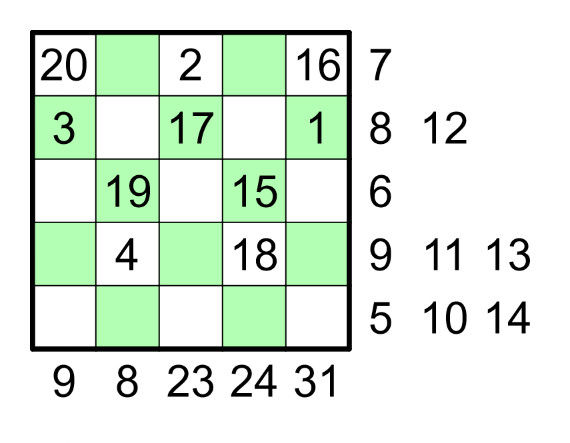
You can solve the problem via integer linear programming as follows. For $i,j\in\{1,\dots,5\}$ and $k\in\{1,\dots,20\}$, let binary decision variable $x_{ijk}$ indicate whether cell $(i,j)$ takes values $k$. Let $c_j$ be the required sum of column $j$, and let $r_i$ be the required product of row $i$. For prime $p\in\{2,3,5,7,11,13,17,19\}$, let $\nu_p(n)$ be the $p$-adic valuation of $n$, that is, the exponent of $p$ in the prime factorization of $n$. Let $N_{ij}=\{(i',j'):|i-i'| \cdot |j-j'|=2\}$ be the set of knight's move neighbors of cell $(i,j)$. The constraints are \begin{align} x_{1,1,20} &= 1 \tag1\label1 \\ x_{2,5,1} &= 1 \tag2\label2 \\ \sum_k x_{ijk} &\le 1 && \text{for all $i,j$} \tag3\label3 \\ \sum_i \sum_j x_{ijk} &= 1 && \text{for all $k$} \tag4\label4 \\ \sum_i \sum_k k x_{ijk} &= c_j && \text{for all $j$} \tag5\label5 \\ \sum_j \sum_k \nu_p(k) x_{ijk} &= \nu_p(r_i) && \text{for all $i, p$} \tag6\label6 \\ x_{ijk} &\le \sum_{(i',j') \in N_{ij}} x_{i',j',k+1} && \text{for all $i,j$ and $k < 20$} \tag7\label7 \end{align} Constraints \eqref{1} and \eqref{2} enforce the given locations of $20$ and $1$. Constraint \eqref{3} assigns at most one value to each cell. Constraint \eqref{4} assigns each value to exactly one cell. Constraint \eqref{5} enforces the column sums. Constraint \eqref{6} enforces the row products. Constraint \eqref{7} enforces the knight's move restriction.

The unique solution turns out to be

\begin{matrix} 20 &. &2 &7 &16 \\3 &8 &17 &12 &1\\. &19 &. &15 &6\\9 &4 &13 &18 &11\\. &. &10 &5 &14\end{matrix}